卡尔曼滤波的由来
卡尔曼滤波的应用
卡尔曼滤波最为人们津津乐道的应用，便是用于了将阿姆斯特朗送上月球的阿波罗飞船的导航计算机。
经典卡尔曼滤波
小车的一维定位问题
考虑一个小车的一维定位问题：
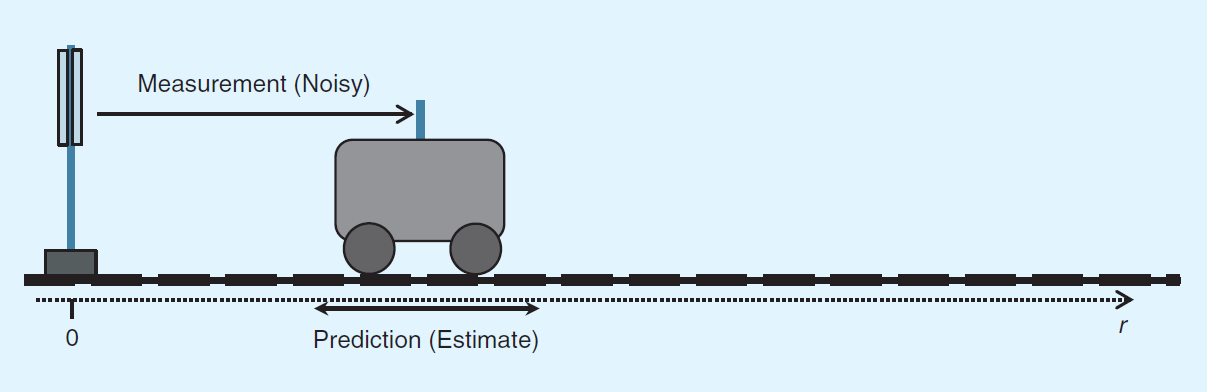如上图所示，小车在一条直线上向右匀速行驶，在左侧定义了一个坐标原点，并在坐标原点出架设了一套测量装置，测量装置没隔一定的时间间隔就对小车离原点的位置和速度进行测量。定义描述小车状态的的状态向量
经典卡尔曼滤波的数学抽象
前提假设
公式推导
预测：
$$ x^{\prime}=F x+u $$
$$ P^{\prime}=F P F^{T}+Q $$
观测更新： $$ y=z-H x^{\prime} $$
$$ S=H P^{\prime} H^{T}+R $$
$$ K=P^{\prime} H^{T} S^{-1} $$
$$ x=x^{\prime}+K y $$
$$ P=(I-K H) P^{\prime} $$